24. Refresh on Confusion Matrices
Confusion Matrices
In Luis's Evaluation Metrics section, we learned about confusion matrices, and if you need a refresher, the video is below.
Confusion Matrix-Question 1
Type 1 and Type 2 Errors
Sometimes in the literature, you'll see False Positives and True Negatives as Type 1 and Type 2 errors. Here is the correspondence:
- Type 1 Error (Error of the first kind, or False Positive): In the medical example, this is when we misdiagnose a healthy patient as sick.
- Type 2 Error (Error of the second kind, or False Negative): In the medical example, this is when we misdiagnose a sick patient as healthy.
But confusion matrices can be much larger than
2 \times 2. Here's an example of a larger one. Let's say we have three illnesses called A, B, C. And here is a confusion matrix:
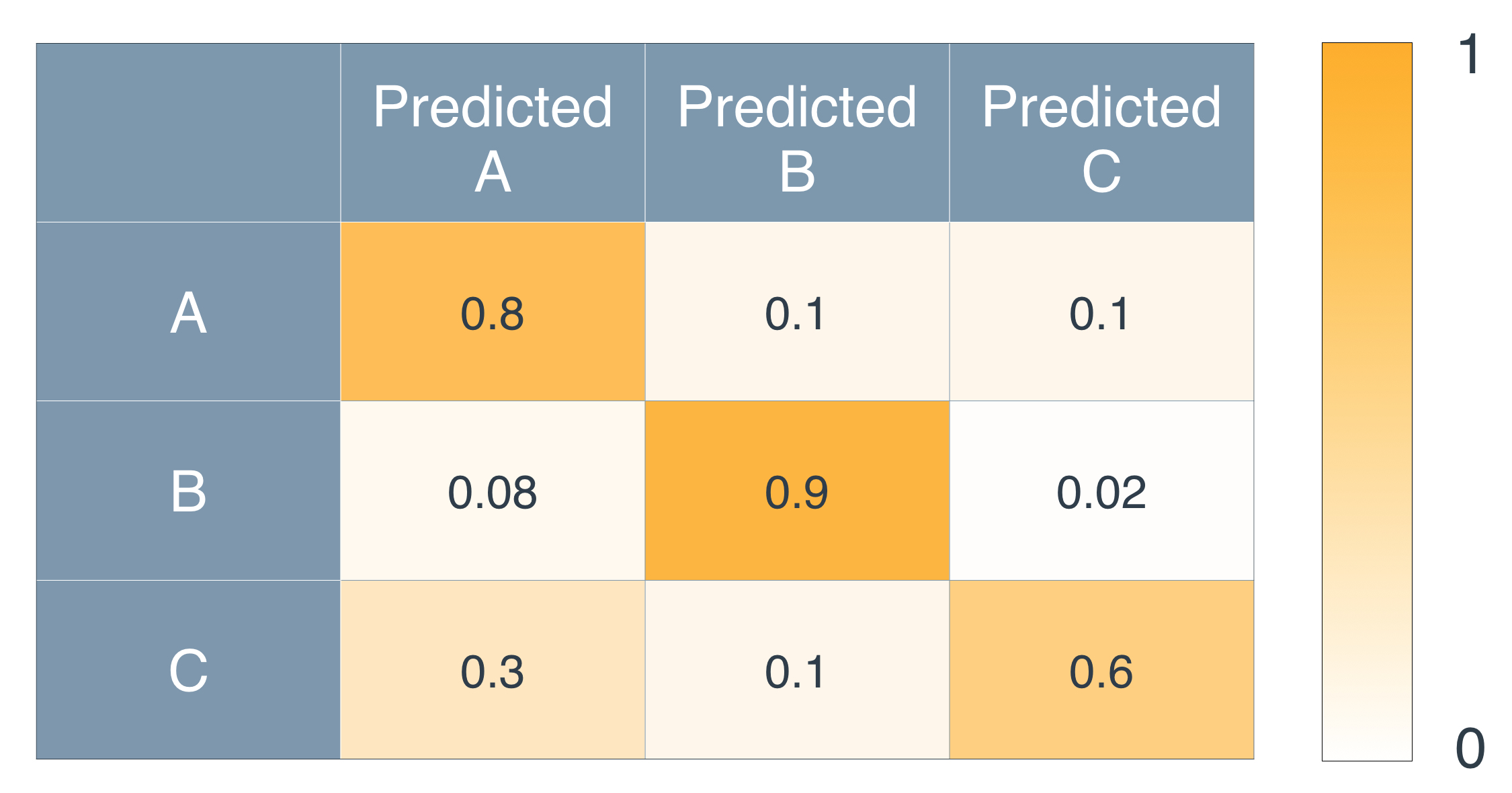
A confusion matrix for three types of illnesses: A, B, and C
As you can see, each entry in the
i-th row and the
j-th column will tell you the probability of the patient having illness
i and getting diagnosed with illness
j.
For example, from the entry on the second row and the first column, we can determine that if a patient has illness B, the probability of getting diagnosed with illness A is exactly 0.08.
Now, let's test our knowledge with some quizzes.
Quiz 1
SOLUTION:
0.1Quiz 2
SOLUTION:
0.4Quiz 3
SOLUTION:
The identity matrixQuiz 4
SOLUTION:
All 1's in the second column, zeros everywhere elseQuiz 5
SOLUTION:
- Every entry is between 0 and 1
- The entries in every row must add to 1